SiteSym - Site-Symmetry method
| Author: | Danel Orobengoa |
|---|---|
| Contact: | bcborgud@lg.ehu.es |
| Web site: | http://www.cryst.ehu.es |
Description
This program implements the so-called site-symmetry approach. The method establishes symmetry relations between the localized states (local atomic displacements) and crystal extended states (phonons, electrons, etc.) over the entire Brillouin zone. The method is based on the procedure of induction of representations of the space group of the crystal from the irreps of the site-symmetry groups of constituent units (atoms, clusters and layers) according to which the local excitations are transformed.
Input data
Step 1:
- Enter the space group number as given in International Tables for Crystallography vol A (referred to as ITA) or choose it from the table of space groups.
- Choose the reciprocal basis for the k-vector, either primitive (as given in Cracknell, A. P., Davies, B. L., Miller, S. C., and Love, W. F. (1979). Kronecker Product Tables. Vol. 1.) or dual to the conventional (ITA).
- Enter the k-vector coordinates and its label.
Step 2:
- Check one Wyckoff positions of the selected space group.
Step 3:
- Select one representative for each chosen Wyckoff position.
Examples and screenshots
Step 1:
- Space Group: 115
- Reciprocal basis: primitive
- k-vector: 1/2, 1/2, 0
- Label: M
This is the look and feel of the first form. The user must specify the space group number and the k-vector. In order to specify the k-vector, 3 coordinates must be introduced apart from its label. The basis to which the coordinates refer (primitive or dual to conventional) must be chosen as well.
 |
Step 2:
- Wyckoff position: 2g
As a result the program returns a form with all the Wyckoff positions of the selected space group. The user must choose one of the positions.
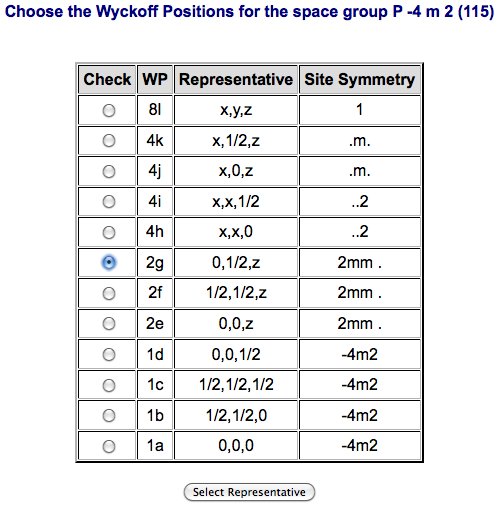 |
Step 3:
- Representative: 0, 1/2, z
On the last form of the program the user is asked to choose one of the possible representatives for each of the Wyckoff positions that were chosen on the preceding step.
 |
Output:
As a result, a series of several tables are shown by the program. First of all a table that shows the site symmetry group for the chosen representative of the Wyckoff position. Note that each element of this group is named as gn, where n goes from 1 to N, the number of elements. If more than one Wyckoff positions were selected on the second form, several tables will appear on this section.
 |
The next two tables are the character tables. First, the character table for the point group of the selected Wyckoff position is shown; the irreps - irreducible representations - are written in Millikan notation. Next, the character table for the calculated site-symmetry group and the selected k-vector appear. The notation of this character table refers to the label of the k-vector and the names given to the site-symmetry group elements on the previous table.
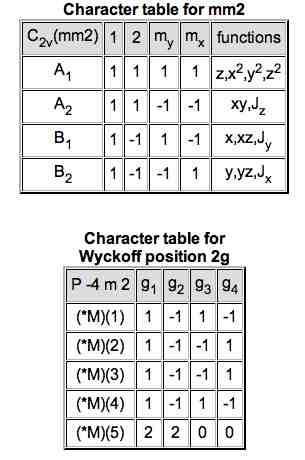 |
Finally, the subduction and induction tables are shown.
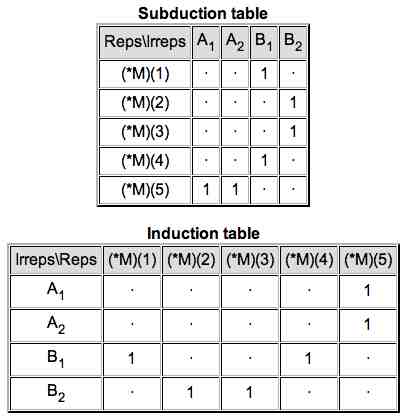 |