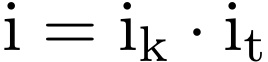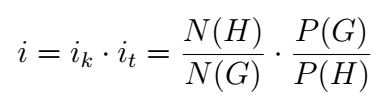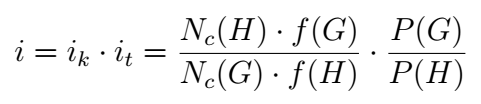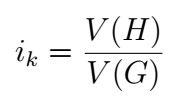For each pair of space groups G > H, a uniquely defined space group M exists such that H ≤ M ≤ G where:
- M is a t-subgroup (translationengleich subgroup) in G: [ it ] is the t-index of M in G
- H is a k-subgroup (klassengleich subgroup) in M: [ ik ] is the k-index of H in M
M is the so-called Hermann group.
As a consequence of Hermann Theorem one can distinguish between three types of subgroups:
- t-subgroups (also called translation equivalent subgroups):
If H is a t-subgroup of G means that T(H) = T(G), i.e. the translation groups of G and H are the same.
The subgroup H loses rotation type operations with repect to G and therefore the point group P(H) < P(G)
M coincides to H.
- k-subgroups (also called point group equivalent subgroups):
If H is a k-subgroup of G means that P(H) = P(G), i.e. the point groups P(G) and P(H) are the same.
The subgroup H loses translation type operations with repect to G and therefore the translation group T(H) < T(G)
M coincides to G.
- general type subgroups: T(H) < T(G) and P(H) < P(G) and so, H < M < G
As consequence a maximal subgroup is always or t-subgroup or k-subgroup of the initial group.
The index of a transformation in a group-subgroup (G > H) relation can be factorized in two parts according to the Hermann theorem.
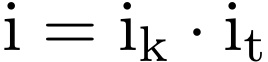
In the formula, [ ik ] is the k-index (the klassengleich index), which coincides with the cell multiplication in the subgroup in the case of primitive cells, and [ it ] (the translationengleich index), which is equal to the ratio between the orders of the point groups of G and H.
In terms of the corresponding indices:
- t-subgroups (called also translation equivalent subgroups): ik = 1, then i = it
- k-subgroups (called also point group equivalent subgroups): it = 1, then i = ik
- general type subgroups: ik ≠ 1 and it ≠ 1
An alternative notation in use for [ ik ] is [ iL ] and for [ it ] is [ iP ].
The index of a transformation is related to the number of atoms of the two structures whose symmetry groups are group-subgroup related.
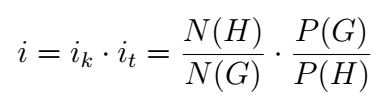
In the given formula [ i ] is the index of the transformation, |P(G)| and |P(H)| are the orders of the point groups of the corresponding space groups G and H, and N(G) and N(H) are the number of atoms per primitive unit cell of two structures with symmetry groups G and H. This expression can also be rewritten as:
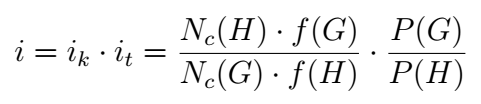
where Nc(G) and Nc(H) are the number of atoms per conventional unit cell of two structures with symmetry groups G and H, and f is the so-called centring factor (f=1 for primitive lattices, 2 for I-, C-, B-, A-centred, 3 for R-centred and 4 for F-centred latttice).
Neglecting lattice deformation, the index [ ik ] can also be expressed as the ratio of volume of the primitive unit cell of H and G:
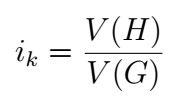
Example 1:
Consider the phase transition between tetragonal P4mm (No. 99) and cubic Pm-3m (No. 221) structures of BaTiO3. The number of atoms per conventional unit cell are equal to Nc(G) = Nc(H) = 5. The two phases are group-subgroup related, and a valid index for this transformation according to the formula is equal to the ratio between the orders of the point groups |P(G)| / |P(H)| (the order of a point group is just the number of the elements of the point group). The ratio between the orders of the point groups can be obtained from the program POINT. The valid index for this transformation is 6.
[ Check the P4mm subgroups of space group Pm-3m with index 6 ]
Example 2:
Consider the group-subgroup related phase transition between orthorhombic Pnma (No. 62) and Pna21 (No. 33) phases of K2SeO4. The number of atoms per conventional unit cell for the given structures are Nc(G) = 28 and Nc(H) = 84. The orders of the point groups are |P(G)| = 8 and |P(H)| = 4. A simple application of the formula gives an index 6 for this transformation.
The index [ ik ] can also be calculated in this case through the ratios of the volume of the primitive unit cell of the group and the subgroup:
- Lattice parameters of K2SeO4 - Pnma: 7.605 10.383 5.949 90 90 90 and V(G) = 469.75 A3
- Lattice parameters of K2SeO4 - Pna21: 22.716 10.339 5.967 90 90 90 and V(H) = 1401.41 A3
[ Check the Pna21 subgroups of space group Pnma with index 6 ]
Example 3:
Consider the group-subgroup related phase transition between monoclinic C2/c (No. 15) and P21/c (No. 14) phases of CaTiSiO5. The number of atoms per conventional unit cell for the given structures are Nc(G) = 32 and Nc(H) = 32. A simple application of the formula gives an index 2 for this transformation.
[ Check the P21/c subgroups of space group C2/c with index 2 ]
- Orientational (twin) domain states: As a consequence of a lost of rotational elements
- Antiphase domain states: As a consequence of a lost of translational elements
[ it ] is the number of twin domain states and [ ik ] is the number of antiphase domain states.
Example 1:
Quartz P6222 (No. 180) > P3221 (No. 154) with index 2
ik = 1 , i = it = 2. P3221 is a t-subgroup of P6222. Two twin domain states.
[ Check the t-subgroups of space group P6222]
Example 2:
Cu3Au: Fm-3m (No. 225) > Pm-3m (No. 221) with index 4
it = 1 , i = ik = 4. Pm-3m is a k-subgroup of Fm-3m. Four antiphase domain states.
[ Check the k-subgroups of space group Fm-3m ]
Example 3:
β - Gd2(MoO4)3: P-421m (No. 113) > Pba2 (No. 32) with index 4
it = 2 , ik = 2. Pba2 is a general type subgroup of P-421m. Two twin domain states with two antiphase domain sates for each twin.
 Help
Help
 Help
Help