LSiteSym - Site-Symmetry method apply to layer groups

Description

This program implements the so-called site-symmetry approach. The method establishes symmetry relations between the localized states (local atomic displacements) and crystal extended states (phonons, electrons, etc.) over the entire Brillouin zone. The method is based on the procedure of induction of representations of the layer groups of the crystal from the irreps of the site-symmetry groups of constituent units (atoms, clusters and layers) according to which the local excitations are transformed.

Input data

Step 1:

Enter the layer group number as given in International Tables for Crystallography vol E (referred to as ITE) or choose it from the table of layer groups.

Step 2:

Check one Wyckoff positions of the selected layer group.

Step 3:

Select one representative for each chosen Wyckoff position.

Step 4:

Enter the k-vector coordinates (k₁, k₂) and its label.

Example

Step 1:

Layer Group: p4/mmm (No. 61)

This is the look and feel of the first form. The user must specify the layer group number.

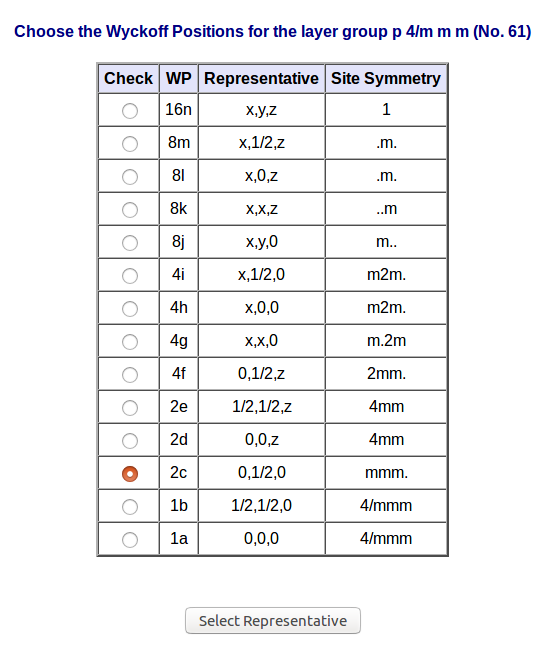
Step 2:

Wyckoff position: 2c

As a result the program returns a form with all the Wyckoff positions of the selected layer group. The user must choose one of the positions.

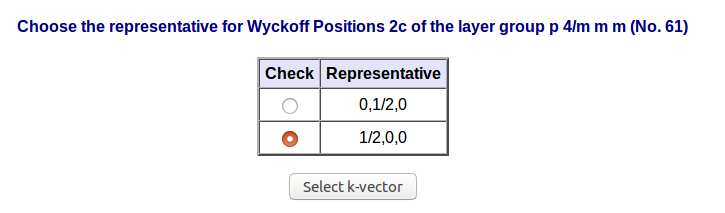
Step 3:

Representative: 0, 1/2, 0

On the next form of the program the user is asked to choose one of the possible representatives for the Wyckoff positions that was chosen on the preceding step.

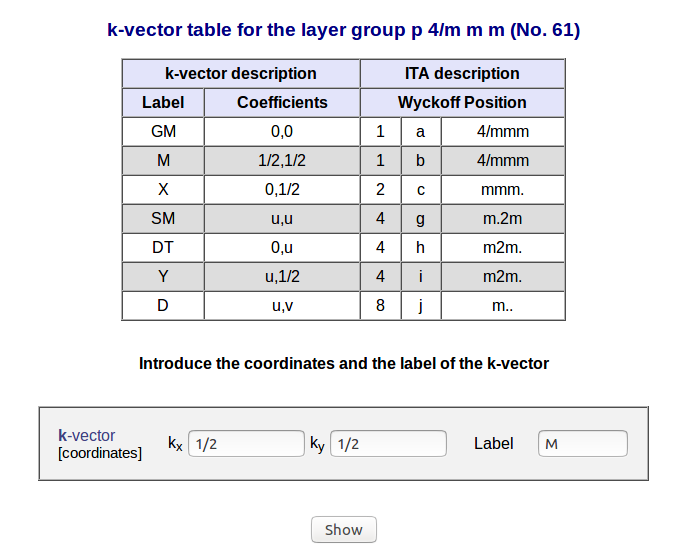
Step 4:

k-vector: k=M(1/2,1/2)

On the last form of the program the user is asked to specify the k-vector, 2 coordinate must be introduced apart from its label. The k-vector table for the chosen layer group is given.

Output:

As a result, a series of several tables are shown by the program. First of all a table that shows the site symmetry group for the chosen representative of the Wyckoff position. Note that each element of this group is named as g_n, where n goes from 1 to N, the number of elements.

The next two tables are the character tables. First, the character table for the point group of the selected Wyckoff position is shown; the irreps - irreducible representations - are written in Millikan notation. Next, the character table for the calculated site-symmetry group and the selected k-vector appear. The notation of this character table refers to the label of the k-vector and the names given to the site-symmetry group elements on the previous table.

Finally, the subduction and induction tables are shown.
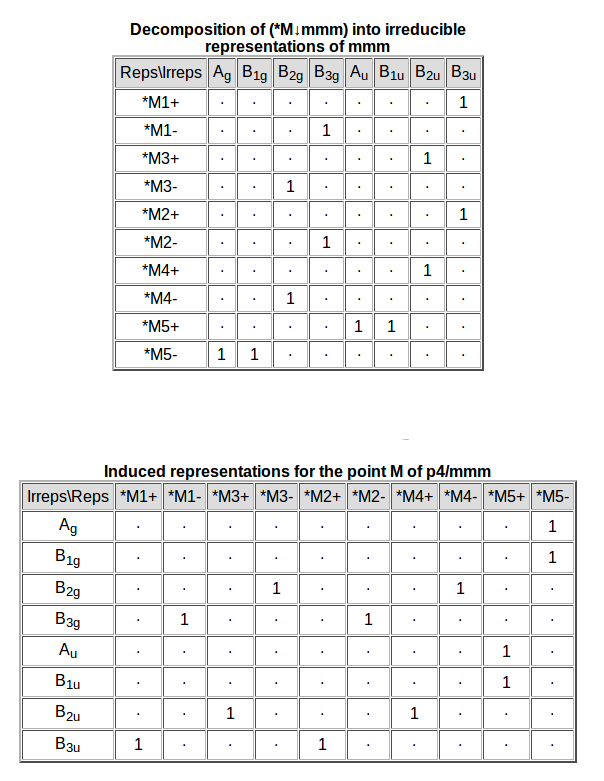